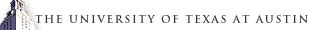Group members
Naman Katyal, Jiyoung Lee, Mai Nguyen, Sung Hoon Jung
Limits of Molecular Dynamics
Long time dynamics (LTD) refers to the dynamic simulation of physical and chemical processes over a time scale which is much longer than can be reached with traditional molecular dynamics. Molecular dynamics simulates dynamic processes by solving Newtonian equation of motion via finite difference approximation. The time step is typically at the femto-second level. Therefore, molecular dynamics can only simulate events efficiently up to pico- or nano-seconds. However, a lot of interesting events, such as diffusions and chemical reactions, can only happen at the time scale of milli-seconds, seconds or even hours or days. Those events are usually called "infrequent", "rare", or "slow" events. Obviously, it would take an enormous number of steps to simulate rare events with molecular dynamics.
Adaptive kinetic Monte Carlo
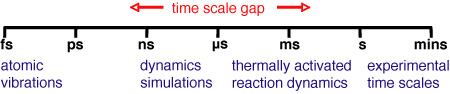
The key step in KMC-hTST simulations is to build a reliable event table for each state the system visits. It is rare that those events in the table can be known beforehand (except for some simple systems). In most cases, the event table has to be built on the fly (or adaptively) for each specific state. We call this type of long time scale simulation "adaptive kinetic Monte Carlo".
Transition State Theory
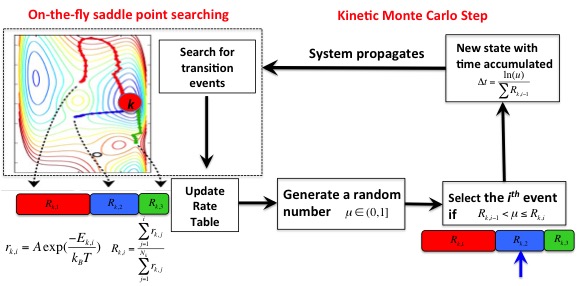
 The potential energy surface (PES) is a multi-dimensional surface on which each energy point corresponds to a possible configuration of the system. There are regions where the system spends most of its time. Those regions are usually local minima or low energy areas corresponding to stable system configurations (e.g., a stable particle, a favorable adsorbate conformation etc). Meanwhile, there are also regions the system rarely visits. From the view of dynamics on the PES, system usually vibrates around those local minima (or basin areas), while it occasionally hops from one local minimum to another. That hopping should contribute most to the LTD process.
The potential energy surface (PES) is a multi-dimensional surface on which each energy point corresponds to a possible configuration of the system. There are regions where the system spends most of its time. Those regions are usually local minima or low energy areas corresponding to stable system configurations (e.g., a stable particle, a favorable adsorbate conformation etc). Meanwhile, there are also regions the system rarely visits. From the view of dynamics on the PES, system usually vibrates around those local minima (or basin areas), while it occasionally hops from one local minimum to another. That hopping should contribute most to the LTD process.
Transition state theory (TST) assumes that system has to cross over some transition state (usually a narrow bottle-neck type of high energy region on the PES) which the system rarely visits, to move from one local minimum to another. TST uses a statistical estimation of how fast the transition is in terms of a rate constant at a certain temperature. For a lot of solid systems, a harmonic approximation (hTST) can be assumed for both minima and transition states. Then, hTST can give a most probable transition pathway (minimum energy path or mechanism) which connects two local minima via a saddle point. The rate of the transition can be calculated from the energies and normal modes of both local minimum and saddle point. By that means, hTST provides a solution to simulate rare events -- the most important part of LTD . Combined with molecular dynamics simulation of frequent evens, a multiple time scale of LTD can be achieved with good efficiency.
Kinetic Monte Carlo
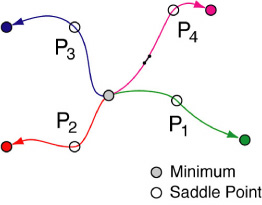
Combined with hTST, kinetic Monte Carlo (KMC) simulation is very useful in long time scale dynamics. Given those rate constants calculated from transition state theory, KMC can build an event table with all the transition mechanisms (for rare events). An event can be selected from Boltzman distribution by generating a random number; fast events have larger rate constants and therefore, are more probable to be chosen. The system configuration will be updated to the end point of the chosen minimum energy pathway. The whole process is repeated for the new state. By this means, the evolution of the system on the PES can be efficiently simulated over a long time scale.
Saddle point searching methods
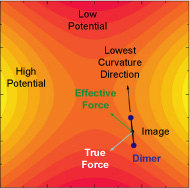
By now, the whole LTD problem has been reduced to finding those saddle points for a given configuration. There are quite a few methods for finding saddle points. Our choice is the Dimer Method developed by Henkelman and Jónsson. It's a minimum-mode-following method using only the first derivative of the potential.
Empirical potentials and DFT
Adaptive kinetic Monte Carlo (aKMC) simulation based on dimer method requires an accurate evaluation of the system energy and forces on atoms. Based on how energy and forces are calculated, aKMC can be carried out through either empirical potentials or first principle methods such as density functional theory. Our group has developed the EON software for running aKMC simulation either with empirical potentials or coupled to density functional theory.
References
R. Garza, J. Lee, M. Nguyen, A. Garmon, D. Perez, M. Li, J. Yang, G. Henkelman, and W. Saidi, Atomistic mechanisms of binary alloy surface segregation from nanoseconds to seconds using accelerated dynamics, J. Chem. Theory Comput. 18, 4447-4455 (2022).L. Li, X. Li, Z. Duan, R. J. Meyer, R. Carr, S. Raman, L. Koziol, and G. Henkelman, Adaptive Kinetic Monte Carlo Simulations of Surface Segregation in PdAu Nanoparticles, Nanoscale 11, 10524-10535 (2019).
S. T. Chill and G. Henkelman, Molecular dynamics saddle search adaptive kinetic Monte Carlo, J. Chem. Phys. 140, 214110 (2014).
S. T. Chill, M. Welborn, R. Terrell, L. Zhang, J.-C. Berthet, A. Pedersen, H. Jónsson, G. Henkelman, EON: Software for long time simulations of atomic scale systems, Model. Simul. Mater. Sci. Eng. 22, 055002 (2014).
R. Terrell, M. Welborn, S. T. Chill, and G. Henkelman, Database of atomistic reaction mechanisms with application to kinetic Monte Carlo, J. Chem. Phys. 137, 014105 (2012). L. Xu, D. Mei and G. Henkelman, Adaptive kinetic Monte Carlo simulation of methanol decomposition on Cu(100), J. Chem. Phys., 131, 244520 (2009).
A. Pedersen, G Henkelman, J. Schiøtz, and H. Jónsson, Long time scale simulation of a grain boundary in copper, New J. Phys. 11, 073034 (2009).
D. Mei, L. Xu and G. Henkelman, Potential energy surface of methanol decomposition on Cu(110), J. Phys. Chem. C 113, 4522 (2009).
L. Xu and G. Henkelman, Adaptive kinetic Monte Carlo for first-principles accelerated dynamics, J. Chem. Phys. 129, 114104 (2008).
G. Henkelman and H. Jónsson, Multiple time scale simulations of metal crystal growth reveal importance of multi-atom surface processes, Phys. Rev. Lett., 90, 116101 (2003).
G. Henkelman and H. Jónsson, Long time scale kinetic Monte Carlo simulations without lattice approximation and predefined event table, J. Chem. Phys., 115, 9657 (2001).